This article is strongly related to my school, other people are not expected to find this very useful, so no translation intended.

本文首发于 LUG Planet ，内容可能有细小不同。

开始

身为某世界一流退学的学生，大物实验自然是逃不过。本人有幸选择了大物实验最多的专业方向，从一级做到六级，直到上学期刚刚结束。大物实验里数据处理是占了很多时间的，那么怎么才能“优雅”地完成这一工作呢？

大一的时候讲座推荐的软件是 Origin ，画图、拟合等虽然方便，但完全鼠标操作，并且只有 Windows 上能运行，Wine 上有时会遇到个别功能不好用，很影响体验（当时我的电脑配置不好，玩不起虚拟机）。思来想去，还是觉得 Python 比较自然，于是故事就这样开始了。

在一级、二级大物中，需求基本是：散点画图（有时是对数）、线性拟合、组合的画图，以及不确定度计算和一般的数值计算。输入输出方面，要手工输入有时候多达几页的手写数据，画出来的图打印上交、计算出的结果手写进实验报告。

Python 做这些事情其实都不困难。画图用 Matplotlib 非常方便，也可以直接保存图片。数据计算自然是 NumPy。线性拟合的话，最初选择了 SciPy。输入输出还是比较基本，从文件读入。

于是，第一个实验，自由落体，的数据和处理就是这样：

#光电门间距 H cm 
#数量级
e -2
90.0	90.0	90.0	80.0	80.0	80.0	70.0	70.0	70.0	60.0	60.0	60.0	50.0	50.0	50.0	40.0	40.0	40.0	30.0	30.0	30.0	20.0	20.0	20.0
#时间差 t ms
e -3
331.6	331.5	331.8	307.9	307.9	307.9	282.9	282.8	282.9	255.8	255.7	255.7	226.9	227.0	226.9	195.2	195.2	195.2	159.9	159.9	159.8	119.2	119.1	119.2

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import math
#avoid font problem
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False 
#read data
data = []
#order of magnitude
oom = 0
fin = open('./data.txt', 'r')
for i in fin.readlines():
    if i[0] == '#':
        #line start with # is comment
        pass
    elif i[0] == 'e':
        oom = int(i.split()[1])
    else:
        data.append(np.array([float(x) * pow(10, oom) for x in i.split()]))
        oom = 0
# print(data)
### main processing ###
l = len(data[0])
x = data[1]
y0 = data[0]
data.append(y0 / x)
y1 = data[2]
slope, intercept, r_value, p_value, std_err = stats.linregress(x, y1)
# z = np.polyfit(x, y1, 1)
s_slope = slope * math.sqrt((r_value ** -2 - 1) / (l - 2))
s_intercept = s_slope * math.sqrt(np.mean(x ** 2))
print('linear regression:' )
print('slope:', slope)
print('intercept:', intercept)
print('r-value:', r_value)
print('p-value:', p_value)
print('std-err:', std_err)
print('r-squared:', r_value ** 2)
print('斜率标准差:', s_slope)
print('截距标准差:', s_intercept)
print('算得重力加速度:', 2 * slope)
#plot
plt.scatter(x, y1, marker='*', color='black', label='原始数据')
# plt.plot(x, y1, '--', color='green', label='光滑曲线')
plt.plot(x, intercept + slope * x, 'r', label='拟合直线')
plt.xlabel('时间 t/s')
plt.ylabel('平均速度 H/t / m/s')
plt.legend(loc=4)
plt.title('小球下落平均速度与时间关系图')
plt.savefig('pic.png')
plt.show()

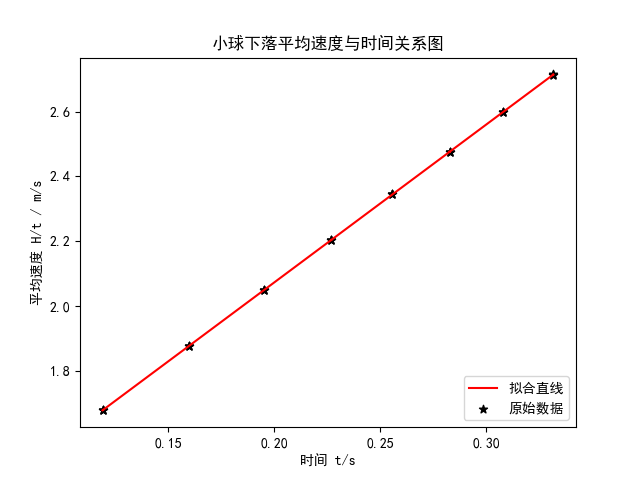
只是画了张图就这么麻烦，很明显，除了练习了 Python 之外，和 Origin 相比生产力负提升。

之后的问题就是简化这些过程了。

两年之后

经过一年多的开发，我将一些常用的画图和数据处理操作打包成库，并添加了方便的文件输入和自动生成 docx 文件的功能。同时将 Python 包 physicsexp 发布到了 PyPI 。

这里以三级大物 β 射线吸收为例，比如，读入文件现在只需要这样：

fin = open('./data.txt', 'r', encoding='utf-8')
pos = readoneline(fin)
N = readoneline(fin)
Al_num = readoneline(fin)
Cnt = readoneline(fin)
fin.close()

数据做图也只要一行代码，一张图上多个曲线也只是一个参数的事，比如这是一张有三条线的图：

simple_plot(Momentum, Emeasure, show=0, issetrange=0, dot='+', lab='测量动能')
simple_plot(Momentum, Eclassic, show=0, issetrange=0, dot='*', lab='经典动能')
simple_plot(Momentum, Erela, dot='o', save='1.png', issetrange=0, xlab='$pc/MeV$', ylab='$E/MeV$', title='电子动能随动量变化曲线', lab='相对论动能')

画图并线性拟合也是非常常见的操作，于是也加入了库：

slope, intercept = simple_linear_plot(Al_Real, CntLn, xlab='质量厚度$g/cm^{-2}$', ylab='选区计数率对数(射线强度)', title='半对数曲线曲线', save='3.png')
print(-slope)
print(math.log(1e4) / (-slope))
print((math.log(Cnt[0]) - 4 * math.log(10) - intercept) / slope)

最后，一行代码将所有的数据和图片生成直接可以打印的 docx 文件，包含名字和日期：

gendocx('gen.docx', '1.png', '2.png', '3.png', 'slope, intercept: %f %f' % (slope, intercept))

文件如图所示，可以直接拿去打印了：

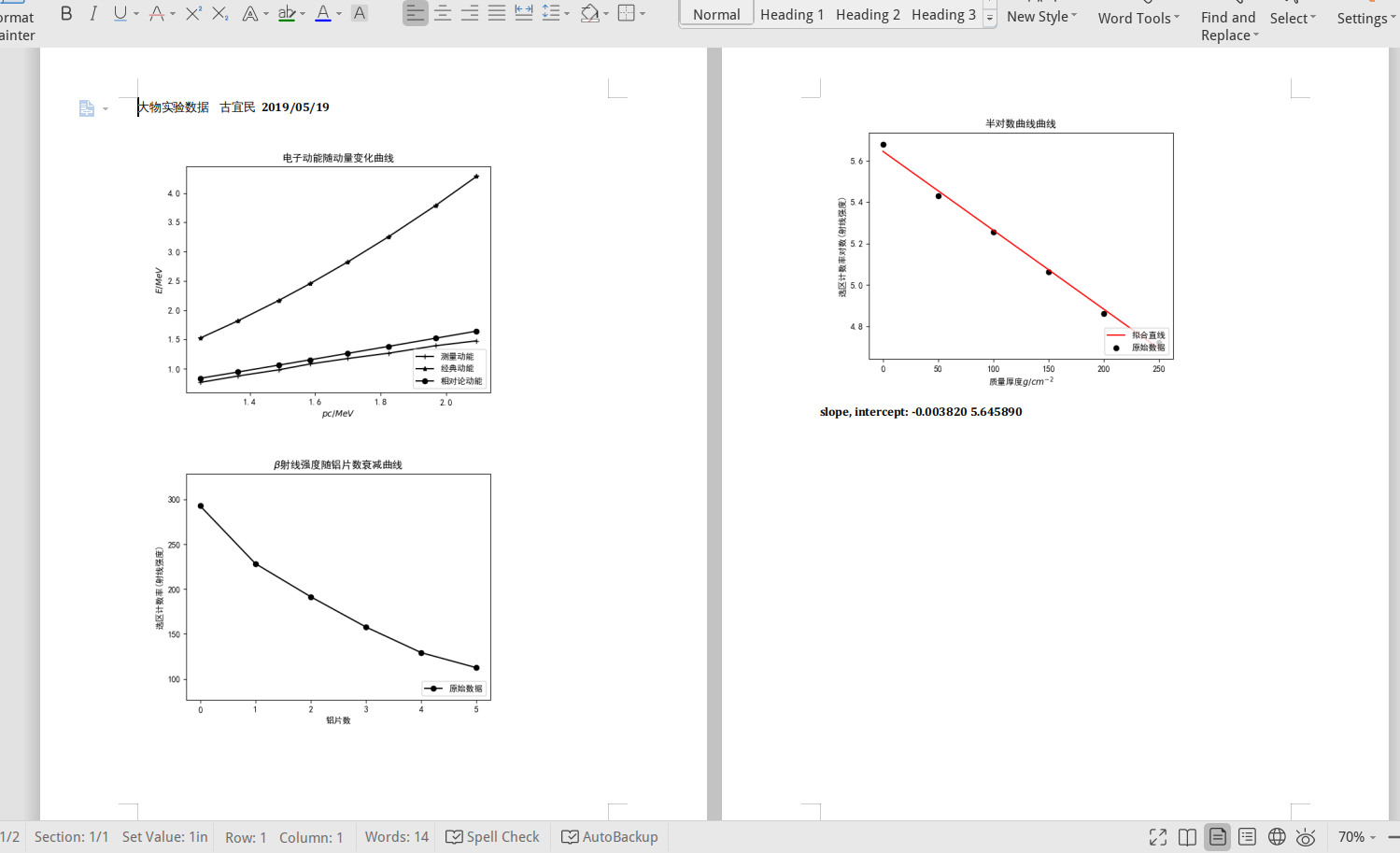
下面是整体代码：

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

from physicsexp.mainfunc import *
from physicsexp.gendocx import *

# read data
fin = open('./data.txt', 'r', encoding='utf-8')
pos = readoneline(fin)
N = readoneline(fin)
Al_num = readoneline(fin)
Cnt = readoneline(fin)
fin.close()

# data process

# calculated calibration values in class
a = 2.373e-3
b = -.0161
dEk = .20

c0 = 299792458.
MeV = 1e6 * electron

Emeasure = a * N + b + dEk
x0 = .10
R = (pos - x0) / 2
B = 640.01e-4
Momentum = 300 * B * R
Eclassic = ((Momentum * MeV)**2 / (2 * me * c0**2)) / MeV
Erela = np.array([math.sqrt((i * MeV)**2 + (me * c0**2)**2) - me * c0**2 for i in Momentum]) / MeV
print('pos\t', pos)
print('R\t', R*100)
print('pc\t', Momentum)
print('N\t', N)
print('Eclas\t', Eclassic)
print('Erela\t', Erela)
print('Emes\t', Emeasure)

simple_plot(Momentum, Emeasure, show=0, issetrange=0, dot='+', lab='测量动能')
simple_plot(Momentum, Eclassic, show=0, issetrange=0, dot='*', lab='经典动能')
simple_plot(Momentum, Erela, dot='o', save='1.png', issetrange=0,
            xlab='$pc/MeV$', ylab='$E/MeV$', title='电子动能随动量变化曲线', lab='相对论动能')

Len = 150
Cnt = Cnt / Len
simple_plot(Al_num, Cnt, xlab='铝片数', ylab='选区计数率(射线强度)',
            title='$\\beta$射线强度随铝片数衰减曲线', save='2.png')
CntLn = np.log(Cnt)
# d = 50 mg / cm^2
d = 50
Al_Real = Al_num * d
slope, intercept = simple_linear_plot(Al_Real, CntLn, xlab='质量厚度$g/cm^{-2}$', ylab='选区计数率对数(射线强度)',
                                      title='半对数曲线曲线', save='3.png')
print(-slope)
print(math.log(1e4) / (-slope))
print((math.log(Cnt[0]) - 4 * math.log(10) - intercept) / slope)

gendocx('gen.docx', '1.png', '2.png', '3.png', 'slope, intercept: %f %f' % (slope, intercept))

整个代码不含空行和注释共 46 行，而上面的自由落体代码 45 行。可见包装程度还是不错的。先计算然后画这三张图，写上面的代码和 Origin 相比哪个更快呢？还是看个人习惯，反正我是比较习惯代码。至少，这说明了大物实验需要的数据处理还是有很多相似点的，以至于打包一些函数可以提高一些生产力。

你可能会问，为什么没有误差分析的功能。这确实是一个问题：计算 A 类和 B 类不确定度等不同实验差别很大，水平有限，我能做的除了将常数打表提供最基础的功能外，好像就没什么了。并且，开发得差不多时已经到二级中期了，算不确定度也不常见了（所以，别被一级吓怕了），所以这部分也没怎么测试过，属于 TODO 。

迟到的 Jupyter Notebook

以上还是标准的 Python ，但五级大物时，我尝试了仅一次就发现明显 Jupyter Notebook 更适合做类似的工作——尽管它不能用 Vim 编辑代码！这下子，数据直接输入在 Notebook 里就好了，画图也是所见即所得，不用等一张一张弹出来了。而进行临时的运算也不必影响正常流程。如图：

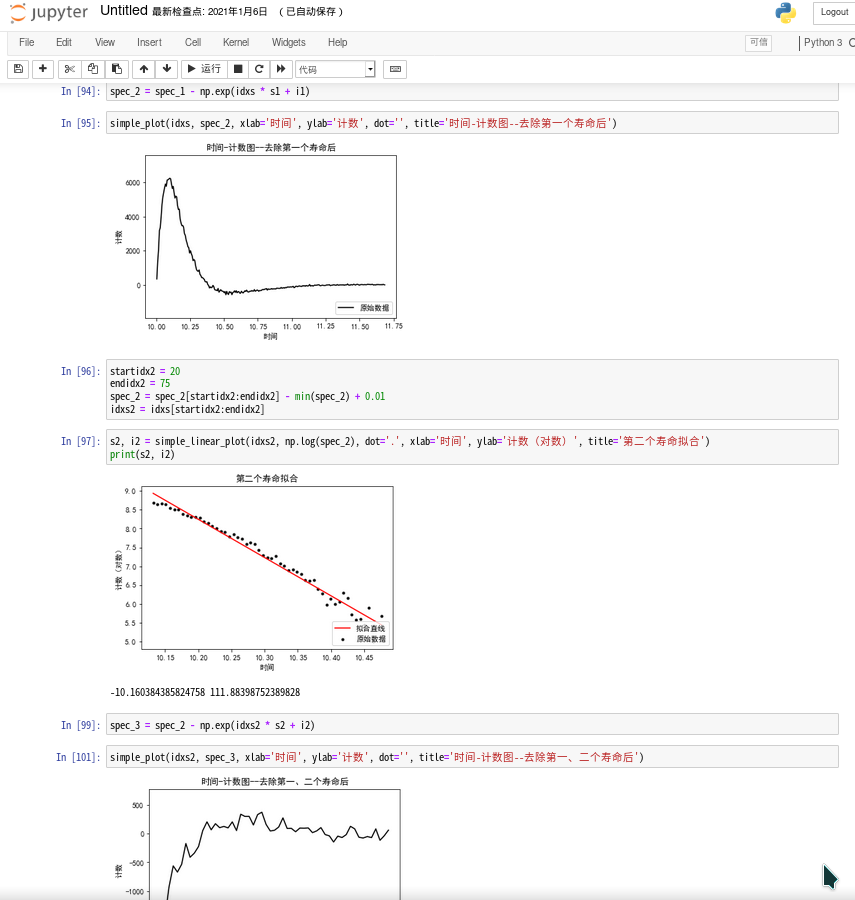
既然都到了 Jupyter ，如果多人合作的话，JupyterHub 是非常不错的选择，可以多个人在一台服务器上使用 Jupyter Notebook 。我之前配置的是每个用户一个隔离的 Docker 容器，里面的 Python 已经装好了包，可以直接使用，同时挂载了一个共享空间可以分享写好的 Notebook 。其实 JupyterHub 有用 Github 帐号登录之类的权限管理功能，但当时我们是几个认识的人合作，就没有管这些。

具体的代码在我的 Github 上，如果有人在写大物实验报告的过程中无聊了想找个地方摸鱼浪费点时间，不妨来看看。

总结

如果您只是想尝试用 Python 处理大物实验数据，我还是可以比较负责地说对于 95% 以上的实验是完全没有问题的。使用 NumPy 和 SciPy 计算， Matplotlib 做图，配以 docx 生成、 Jupyter Notebook 或 JupyterHub 团队合作，可以比较轻松地完成所有需要的操作，并可以通过包装库提高效率。只有个别实验（比如五级大物有实验需要使用 ROOT 处理数据）可能这套流程不是很适合，但问题不大。

之前也有学长学姐尝试过类似的大物实验自动化项目，但因为暂时无法全部找到并对比，这里就不说了。大一的时候确实是想搞一套自动化程度很高的东西，但水平实在有限，并且不同的实验处理过程不太一样，一己之力完成每一个实验专属的程序也不太现实，所以结果就是自己挖了个坑并跳进去出不来：有时想想，或许还是左手卡西欧 991 右手座标纸来得快一些呢！